Formula De Reduccion Integrales
La integración por reducción fórmulas de reducción se aplica a integrales con funciones de exponentes normalmente enteros pero elevado. I n -cos xsen n - 1 x n - 1 sen n - 2 x 1 - sen² xdx.
Integrales como la del ejemplo anterior podrían parecer muy especiales pero ocurren con frecuencia en aplicaciones de integración.
Formula de reduccion integrales. Integración por partes y explica muchos ejemplos y la solución a interrogantes que se pueden dar. 1 Separamos la resta de integrales y sacamos las constantes multiplicativas. La integracin por reduccin se aplica a integrales con funciones de exponentes enteres pero muy grandes buscando obtener una parte integrada y una sin integrar en la que aparecer la misma integral inicial pero con los exponentes disminuidos de esta forma aplicando la frmula se puede ir rebajando el exponente hasta llegar a integrales de resolucin.
I k F X k D X Displaystyle I_ k int f x k text d x dónde. La fórmula 2 disminuye 1 unidad a p y falla cuando npm10. Algo especial en expresiones matemáticas es que el signo de multiplicación puede ser omitido en ocasiones por ejemplo escribimos 5x en lugar de 5x.
Integrales de la forma. Formulario de integrales c 2001-2005 Salvador Blasco Llopis Este formulario puede ser copiado y distribuido libremente bajo la licencia Creative Commons Atribuci on 21 Espana. Formulario de integrales.
La fórmula 3 aumenta n unidades a m y falla cuando m10. U 1 u 2 C. Fórmulas de reducción para diferenciales binomias.
2 Empleamos las fórmulas 1 y 2 para obtener. MOISES VILLENA MUÑOZ La integral Indefinida Objetivo. Demostrar que n Z1 n1cos xdx cosn n1x sin x cosn2 xdx 1n n1 n1sinn xdx sinn1 x cos x sinn2 xdx 2n n1 n2secn xdx secn2 x tan x secn2 xdx 3n1.
La integral de una potencia está dada por la siguiente fórmula x n d x x n 1 n 1 displaystyleint xn dxfrac x n1 n1 x n d x n 1 x n 1 donde n n n representa a un número o función constante como 3 2 frac 3 2 2 3. Se pretende que el estudiante encuentre algebraicamente antiderivadas 11 DEFINICIÓN 12 TÉCNICAS DE INTEGRACIÓN 121 FORMULAS 122 PROPIEDADES 123 INTEGRACIÓN DIRECTA 124 INTEGRACIÓN POR SUSTITUCIÓN 125 INTEGRACIÓN POR PARTES 126 INTEGRALES DE FUNCIONES. La fórmula aplicable en el procedimiento de los porcientos integrales consiste en.
Buscando obtener una parte integrada y una parte sin integrar en la que aparecerá la misma integral pero con estos exponentes disminuidos se aplicará una fórmula que puede ir rebajando el exponente hasta. Para encontrar la fórmula de reducción de I n se integrará por partes. En los próximos días y semanas analizaremos los temas que conciernen a la materia de cálculo integral estos temas son teóricos y prácticos al mismo tiempo puesto que se deben resolver problemas de integrales que a futuro nos servirán en otras materias y a lo largo de nuestra vida laboral.
La fórmula 4 aumenta 1 unidades a p y falla cuando p10. Porciento integral cifra parcialcifra base 100. En otras palabras la fórmula de reducción expresa la integral.
Du n - 1sen n - 2 xcos xdx. 2 Empleamos la fórmula 5 para resolver la segunda integral. Las frmulas de reduccin se utilizan para automatizar el proceso de efectuar sucesivas integraciones por partes.
I norte F X norte D X Displaystyle I_ n int f x n text d x en términos de. Mayo 2001 Tercera revisi on. Sin 1.
Fórmulas de integrales trigonométricas inversas. Febrero 2005 Sexta revisi on. Mayo 2002 Cuarta revisi on.
Fórmulas de reducción para integrales hiperbólicas Obtenido de AnexoFC3B3rmulas de reducciC3B3n para integrales Categorías. Integrando una potencia uniforme de senx. Se pueden determinar mediante métodos similares como resultado de la identidad.
U d u u sin 1. La Calculadora de Integrales tiene que detectar esos casos e insertar el signo de multiplicación. Pensando en esto hemos decidido recopilar.
1 Separamos la resta de integrales. K norte. Por tanto I n -cos xsen n - 1 x - n - 1 -sen n - 2 xcos² xdx.
3 Así el resultado de la integral es. Fórmula para calcular los Porciento Integrales. Factor constante es igual a cien entre la cifra base por cada cifra parcial.
1 El ángulo es. S eptima revisi on. Dificultad de la integral mediante un cambio de variable de tal manera que la integral resultante sea más fácil de integrar ó que sea una integral conocida.
IMPORTANTE En este video veremos un ejemplo resuelto de cómo calcular la integral de una potencia de la función trigonométrica seno sen elevado al expon. Porciento integral es igual a la cifra parcial entre la cifra base por cien. V sen xdx -cos x.
Dv sen xdx. Cos 1. Y se resuelve para la integral requerida se obtiene.
U sen n - 1 x. Julio 2003 Quinta revisi on. Para que la fórmula de cambio de variable tenga posibilidades de éxito debemos identificar en el integrando a una función u y a u su derivada.
Integral indefinida de la secante. 3 Así el resultado de la integral es. U d u u cos 1.
La fórmula 1 disminuye n unidades a m y falla cuando npm10. Son invaluables Estas identidades a veces se conocen como identidades reductoras de potencia y pueden derivarse de la identidad de doble ángulo cos 2x cos² x sen² x y la identidad pitagórica cos² x sen² x 1. Al hacer esto la Calculadora de Integrales tiene que respetar el orden de operaciones.
Este video corresponde al curso de Cálculo Integral.

Integrales Trigonometricas Calculo21
Integrales Por Reduccion Pdf Metodo De Elementos Finitos Ecuaciones

331 Integrales Mediante Formulas De Reduccion Youtube
Integracion Por Formulas De Reduccion Wikipedia La Enciclopedia Libre
Integral De La Secante Cubica Wikipedia La Enciclopedia Libre
Integrales Por Reduccion Pdf Metodo De Elementos Finitos Ecuaciones
Integracion Por Formulas De Reduccion Wikipedia La Enciclopedia Libre

331 Integrales Mediante Formulas De Reduccion Youtube
Integracion Por Formulas De Reduccion Wikipedia La Enciclopedia Libre
Integral De La Secante Cubica Wikipedia La Enciclopedia Libre

331 Integrales Mediante Formulas De Reduccion Youtube
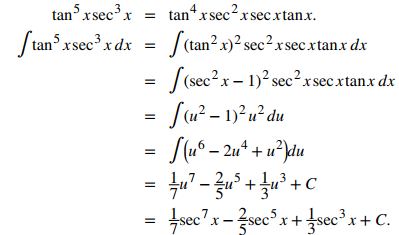
Integrales Trigonometricas Calculo21
Integral De La Secante Cubica Wikipedia La Enciclopedia Libre

Integral De Secante A La N Formula De Recurrencia














Posting Komentar untuk "Formula De Reduccion Integrales"